灰色理论数学模型具有利用部分信息、计算简单等特征, 是我国学者邓聚龙教授提出的, 将模型中无规律的数据进行变换处理成为有序的序列。灰色理论数学模型针对原始数据序列进行累加, 使得数据具有一定的规律性, 再对其进行曲线拟合^[12]。令时间数据序列为x⁰:

x⁰=( xt0|t=1, 2, …, n)=( x10, x20, …, xn0)。 (1)

灰度模型对时间数据序列x⁰做累加后获得新的数据序列x¹, x¹中第t时刻的数据为原始时间数据序列x⁰的前t项数据之和, 即:

x¹=( xt1|t=1, 2, …, n)=( x10, ∑t=11xt0, ∑t=12xt0, …, ∑t=1nxt0)。 (2)

根据获得的新数据序列x¹, 构建微分方程, 得到

dx1dt+ax¹=u。 (3)

式中:a为发展灰数, u为内生控制灰数。

整理方程得到解为:

xt1'= x10-uae^-a(t-1)+ ua。 (4)

xt1'为数据序列x¹的估算值, 再对 xt1'做减法处理得到x⁰的预测值 xt0', 得到

xt0'= xt1'- xt-11'。其中

t=n, n-1, …, 3, 2。 (5)

由此可见, 灰色数学模型是将时间序列数据x⁰直接转换成为微分方程, 利用系统信息进行模型量化, 可以在获得部分信息的情况下进行估算, 获得预测值。

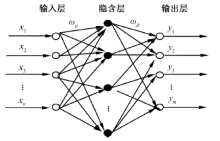
人工神经网络(artificial neural network, ANN)近几年来在人工智能方面得到广泛的应用, 其主要特征为类似人脑的神经元网络对信息进行处理, 按照一定的规律构建模型, 输入层与输出层之间以不同方式组成复杂的网络结构, 具有自适应性和自学习能力的特征。待处理的数据信息从输入层输入, 通过隐含层的计算处理到输出层输出结果, 任何一层的神经元装填及其数据计算结果都会影响后面一层的数据处理结果。通常在输出层和预期的结果进行比较, 根据误差反向传播多次迭代直至达到误差允许范围内, 或者完成设定的迭代次数^[13]。BP神经网络拓扑结构如图1所示。预测函数的自变量为神经网络的输入参数, 函数的因变量为神经网络计算结果的输出值。因此, 神经网络构成的函数映射关系为由n个函数自变量从输入层输入, 产生m计算机结果从输出层输出。

图1

	Figure Option ViewDownloadNew Window
	图1 BP神经网络拓扑结构 x1, x2, …, xn为BP神经网络的输入参数, 神经网络的计算结果表示为Y1, Y2, …, Ym, BP神经网络权值用ω ij和ω jk表示

对于多个变量参数的灰色神经网络模型优化方程可以表示为:

dy1dt+ay₁=b₁y₂+b₂y₃+…+b_n-1y_n。 (6)

式(6)中, y₁为系统模型的输出参数, y₂, y₃, …, y_n为系统模型的输入参数, a, b₁, b₂, …, b_n-1为系统模型的方程系数。其时间相应函数为:

z(t)=y₁(0)e^-at+(1-e^-at) b1ay2(t)+

b2ay3(t)+, …, +bn-1ayn(t)。 (7)

令

d= b1ay₂(t)+ b2ay₃(t)+, …, + bn-1ay_n(t)。 (8)

将式(7)和式(8)整理得到:

z(t)= y1(0)-d-y1(0)×11+e-at+2d×

11+e-at× (1+e^-at)。 (9)

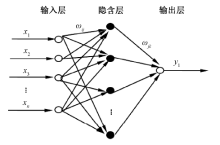
将整理得到的式(9)映射到BP神经网络中, 获得n个输入层参数及1个输出参数预测值的灰色神经网络优化模型, 图2为灰色神经网络拓扑结构图, 根据若干个自变量计算获得1个预测值。

图2

	Figure Option ViewDownloadNew Window
	图2 灰色神经网络拓扑结构 x1, x2, …, xn为模型中的输入参数, ω ij、ω jk模型的权值, 输出层Y1为系统模型的输出参数

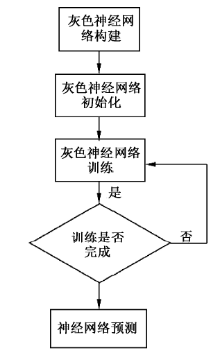
基于灰色神经网络的茶叶产量预测算法模型流程如图3所示。其中, 灰色神经网络构建的输入数据与输出数据确定灰色神经网络的结构。将非自然因素如茶叶采摘面积变化、城市居民茶叶消费价格指数、城镇居民人均可支配收入指数等作为输入数据, 构成三维数组; 预测值为当年的茶叶产量, 为1维数组。

图3

	Figure Option ViewDownloadNew Window
	图3 灰色神经网络模型流程

系统模型以浙江省2001— 2011年的茶叶产量、采摘面积、城市居民茶叶消费价格指数、城镇居民人均可支配收入指数等作为输入数据和输出数据(表1)进行测试。所有数据均通过网络查询《中国年鉴统计数据库》获得, 原始数据均来自历年的《浙江统计年鉴》《中国统计年鉴》。

表1

表1

表1 2001— 2011年浙江省茶叶产量情况 年份 产量/t 面积/103 hm2 价格指数 收入指数 2001 120 600 116.0 104.8 113.3 2002 138 500 119.7 96.5 113.4 2003 132 700 124.1 100.1 111.9 2004 138 700 126.4 98.9 107.4 2005 144 400 133.6 97.2 110.3 2006 152 400 136.8 99.3 110.8 2007 160 229 147.0 99.2 108.4 2008 162 345 154.3 102.9 105.4 2009 167 411 158.3 103.1 109.7 2010 163 000 159.9 106.2 106.9 2011 170 000 164.4 103.4 107.5 注:面积为茶叶采摘面积(103 hm2); 收入指数为城镇居民人均可支配收入指数(上年=100); 价格指数为城市居民茶叶消费价格指数(上年=100)。

表1 2001— 2011年浙江省茶叶产量情况

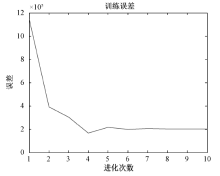
在预测过程中, 特别注意输入和输出数据的选择。本系统模型的训练数据集由2001— 2006年的原始数据组成, 系统模型通过多次迭代后结果如图4所示。

图4

	Figure Option ViewDownloadNew Window
	图4 系统模型多次迭代结果

将训练权值作为对2008— 2011年数据进行预测判断的参数, 并对茶叶预测产量与实际值进行比较, 结果见表2。由表2可知, 本文优化模型2008— 2011年预测产量与实际产量的平均相对误差为1.35%, 2011年预测值与实际值较接近, 而BP神经网络模型预测产量与实际产量的平均相对误差为4.47%, 可见本文优化模型可有效预测茶叶产量, 优化后的系统模型优于现有的BP神经网络算法。

表2

表2

表2 2008— 2011年浙江茶叶预测产量与实际产量 年份 实际 产量/ t 优化模型 BP神经网络模型 预测 产量/t 相对 误差/% 预测 产量/t 相对 误差/% 2008 162 345 164 310 1.21 165 519 1.96 2009 167 411 168 160 0.45 169 760 1.40 2010 163 000 169 030 3.70 179 010 9.82 2011 170 000 170 070 0.04 178 008 4.71

表2 2008— 2011年浙江茶叶预测产量与实际产量

对茶农和经销商等用户而言, 茶叶产量直接影响其经济收入, 而影响茶叶产量的因素较多, 比如:光照、温度、湿度、土壤、虫害及非自然因素等, 众多影响因素导致人们无法很好地估算茶叶产量。本文通过灰度理论结合神经网络系统的适应性及自学习能力, 选取相对容易获得的采摘面积、城市居民茶叶消费价格指数、城镇居民人均可支配收入指数等数据作为估算参数, 通过优化的灰色神经网络模型进行产量预测, 结果表明, 优化后的系统模型能够较好预测当年的茶叶产量。由于提供的历年相关数据量有限, 故其迭代和收敛效果相对偏弱。如果系统模型的训练样本足够, 获得更多历年相关参数, 系统模型的迭代次数、函数的收敛性及预测值的评价误差率可能更优。